Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China

ISBN-13: 9780271012384 / Angielski / Miękka / 1977 / 108 str.

Frank Swetz; T. I. Kao

Opis

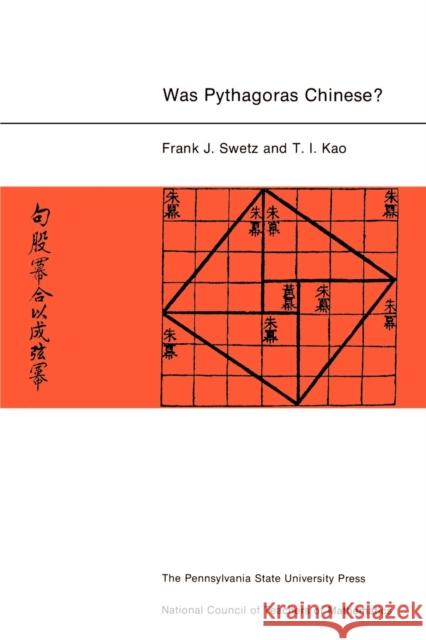
The title of this monograph, while intended to intrigue and attract the otherwise unresponsive reader, is not whimsically conceived. Of course, the historical figure of mathematical fame known as Pythagoras, born on the island of Samos in the 6th century B.C., was Greek, not Chinese. But there is another "Pythagoras" equally deserving fame. He is the man who first proved the proposition that "the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse." For hundreds of years this theorem has borne the name of Pythagoras of Samos, but was he really the first person to demonstrate the universal validity of this theorem? The issue is controversial. Seldom are mathematical discoveries the product of a single individual's genius. Often centuries and thousands of miles separate the appearance and the isolated reappearance of the same mathematical or scientific theory.It is now acknowledged that the "Pascal Triangle" method of determining the coefficients of a binomial expansion was known in Sung China 300 years before Pascal was born, and that the root extraction algorithm credited to the 19th-century British mathematician W. G. Homer was employed by Han mathematicians of the 3rd century A.D. If, then, these mathematical processes are to bear the names of the persons who devised them, surely "Pascal" and "Homer" were Chinese. So too might such an argument be posed for the Pythagorean Theorem on the basis of evidence contained in ancient Chinese mathematics texts. It is the purpose of this monograph to present and examine this evidence. This is a joint publication of the Penn State Press and the National Council of Teachers of Mathematics.Penn State Study No. 40