Representation of Universal Algebra (Russian Edition): Polymorphism

ISBN-13: 9781511464949 / Rosyjski / Miękka / 2015 / 98 str.

Aleks Kleyn

Opis

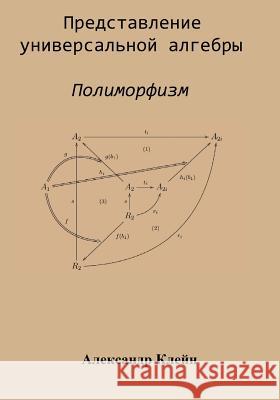
Module is effective representation of ring in Abelian group. Linear map of module over commutative ring is morphism of corresponding representation. This definition is the main subject of the book. To consider this definition from more general point of view I started the book from consideration of Cartesian product of representations. Polymorphism of representations is a map of Cartesian product of representations which is a morphism of representations with respect to each separate independent variable. Reduced morphism of representations allows us to simplify the study of morphisms of representations. However a representation has to satisfy specific requirements for existence of reduced polymomorphism of representations. It is possible that Abelian group is only Ω-algebra, such that representation in this algebra admits polymorphism of representations. However, today, this statement has not been proved. Multiplicative Ω-group is Ω-algebra in which product is defined. The definition of tensor product of representations of Abelian multiplicative Ω-group is based on properties of reduced polymorphism of representations of Abelian multiplicative Ω-group. Since algebra is a module in which the product is defined, then we can use this theory to study linear map of algebra. For instance, we can study the set of linear transformations of D-algebra A as representation of algebra A⊗A in algebra A.